10 Soal & Pembahasan Suhu, Kalor, & Perpindahannya (bagian 2) ǀ Pilihan Ganda
Bab suhu, kalor, dan
perpindahan kalor yang terdiri dari beberapa bahasan, yaitu konversi satuan
suhu, menentukan suhu saat termometer diganti, pemuaian, asas black, kalor, dan
perpindahan kalor. Berikut 10 soal dan pembahasan suhu, kalor dan perpindahannya.
Baca sebelumnya : 10 Soal & Pembahasan Suhu, Kalor, & Perpindahan Kalor (bagian 1) ǀ Pilihan Ganda
Pilihlah jawaban yang
tepat dari pilihan di bawah ini.
11. Logam sepanjang 70 cm
memiliki koefisien muai panjang sebesar 10-5. Jika awalnya logam
bersuhu 132oC, maka panjang logam saat suhunya dinaikkan hingga 287oC
adalah . . .
A. 69,78 cm
B. 69,89
cm
C. 70,11
cm
D. 70,22
cm
E. 70,33 cm
Pembahasan :
Soal menunjukkan benda
memuai (bertambah panjang).
Diketahui :
|
Li |
= |
70
cm |
Tf |
= |
287oC |
|
α |
= |
10-5
/K |
ΔT |
= |
287-132
|
|
Ti |
= |
132oC |
|
|
155
K |
Ditanya : Panjang akhir (Lf)
Lf = Li
+ ΔL
Lf = Li
+ (Li. α. ΔT)
Lf = 70+ (70. 10-5.
155)
Lf = 70+ (0,11)
Lf = 70,11 cm
Jawaban C.
12. Logam dengan luas 25 cm2
dan 75 cm2 diharapkan memiliki perubahan luas yang sama, yaitu
sebesar 0,5 cm2. Perbandingan perubahan suhu yang diberikan adalah .
. .
A. 1/3
B. 1/2
C. 2/1
D. 2/3
E. 3/1
Pembahasan :
Soal menunjukkan benda
memuai (bertambah luas). Benda A dan benda B sejenis, tetapi berbeda ukuran
luas. Mereka dipanaskan pada capaian suhu yang berbeda. Diakhir, pertambahan
luas keduanya ternyata sama besar.
Diketahui :
|
*Benda
A |
*Benda
B |
||||
|
AiA |
= |
25
cm2 |
AiB |
= |
75
cm2 |
Ditanya : Perbandingan
perubahan suhu benda A dan B (ΔTA/ΔTB)
|
ΔAA |
= |
ΔAB |
|
AiA. β. ΔTA |
= |
AiB.
β. ΔTB |
|
AiA. ΔTA |
= |
AiB.
ΔTB |
|
mteh.
ΔT |
= |
mcaramel. ΔT |
|
25. ΔTA |
= |
75.
ΔTB |
|
ΔTA/ ΔTB |
= |
75/25 |
|
ΔTA/ ΔTB |
= |
3/1 |
Jawaban E.
13. Jika logam dipanaskan hingga
mengalami perubahan suhu 50 K, maka ia akan mengalami peningkatan luas sebesar
10%. Jika proses pemanasan dilanjutkan sebesar 75 K lagi, maka luas total logam
tersebut adalah . . .
A. 125 %
B. 150 %
C. 175 %
D. 200 %
E. 225 %
Pembahasan
:
Luas
logam awal (Ai) adalah A. Kondisi pertama, luas bertambah (ΔA1)
sebesar 0,1A saat ΔT1 50o. Kondisi kedua, saat ΔT2
menjadi 125o, pertambahan luasnya adalah (ΔA2). Luas akhir
kondisi dua menjadi Af2 = Ai + ΔA2
Diketahui
:
|
*Kondisi
satu |
*Kondisi
dua |
||||
|
Ai |
= |
A |
Ai |
= |
A |
|
ΔA1 |
= |
0,1A |
ΔT2 |
= |
125 K |
|
ΔT1 |
= |
50 K |
|
|
|
Ditanya
: Luas akhir kondisi dua (Af2)
*Mencari
nilai perubahan luas kondisi dua ΔA2
|
β1 |
= |
β2 |
|
ΔA1/Ai.
ΔT1 |
= |
ΔA2/Ai. ΔT2 |
|
0,1A/A.
50 |
= |
ΔA2/A. 125 |
|
0,1A/
50 |
= |
ΔA2/125 |
|
ΔA2 |
= |
0,1A(125)/50 |
|
ΔA2 |
= |
0,25A |
Jadi,
pertambahan luas logam, jika perubahan suhunya 125 K adalah 25%. Total luasnya
adalah Af2 = Ai + ΔA2 = A + 0,25A = 100% + 25%
= 125%
Jawaban
A.
14. Zat
cair dituangkan penuh ke dalam wadah yang bervolume 2 liter dan dipanaskan
hingga mengalami perubahan suhu 50oC. Jika koefisien muai ruang saja
cair sebesar 2 x 10-4 /K dan koefisien muai panjang wadah sebesar 2 x
10-5 /K, maka volume cairan yang tumpah adalah . . .
A. 14
liter
B. 1,4
liter
C. 0,14
liter
D. 0,014
liter
E. 0,0014
liter
Pembahasan :
Diketahui :
|
*Wadah
cairan |
*Cairan |
|
||||
|
Vi |
= |
2
liter |
Vi |
= |
2 liter |
|
|
γ |
= |
3α |
γ |
= |
2x10-4/K |
|
|
|
= |
6x10-5 /K |
|
|
|
|
|
ΔT |
= |
50 K |
ΔT |
= |
50 |
|
Ditanya : Volume cairan
yang tumpah (volume wadah – volume cairan)
*Volume wadah
Vf = Vi
+ ΔV
Vf = Vi
+ (Vi.γ.ΔT)
Vf = 2 + (2. 6x10-5.50)
Vf = 2 + 0,006
Vf = 2,006
liter
*Volume cairan
Vf = Vi
+ ΔV
Vf = Vi
+ (Vi.γ.ΔT)
Vf = 2 + (2. 2x10-4.50)
Vf = 2 + 0,02
Vf = 2,02 liter
Jadi, volume tumpah =
volume wadah – volume cairan = 2,006 – 2,02 = 0,014 liter
Jawaban
D.
15. Cairan
yang berada di dalam suatu wadah tidak akan tumpah, jika ditempatkan pada wadah
dengan koefisien muai luas-nya setara dengan . . . . koefisien muai volume
cairan.
A. 1/3
B. 2/3
C. 3/2
D. 3/1
E. 1/1
Pembahasan
:
Pada
kasus nomor sebelumnya, kita tahu bahwa cairan tidak akan tumpah jika volume
wadah = volume cairan. Volume awal keduanya sama, perubahan suhu keduanya sama,
maka koefisien muai volume keduanya juga harus sama.
Sekarang, kita akan mencari hubungan antara koefisien muai volume cairan γ dan koefisien
muai luas wadah β
|
γcairan |
= |
γwadah |
|
γcairan |
= |
3αwadah |
|
γcairan |
= |
2(3/2)αwadah |
|
γcairan |
= |
(3/2)βwadah |
|
βwadah |
= |
(2/3) γcairan |
Jawaban B.
16. Perhatikan besaran-besaran
berikut ini!
1) koefisien konveksi termal
2) luas penampang batang
3) perubahan suhu
4) konstanta boltzman
Faktor yang mempengaruhi
besar rambatan kalor secara konveksi ditunjukkan oleh nomor . . .
A. 1, 2, 3
B. 1, 3
C. 2, 4
D. 4 saja
E. Semua benar
Pembahasan
:
Persamaan pada perpindahan
kalor dengan konveksi adalah
H = h.A.ΔT
H = energi (kalor) yang
mengalir tiap detik
h = koefisien konveksi
A = luas penampang
Jawaban
A.
17. Dua
logam dengan ukuran yang sama disambungkan satu sama lain. Ujung logam yang
koefisien konduksi nya (1/4)k memiliki suhu 0oC. Ujung lainnya yang
memiliki koefisien konduksi sebesar k bersuhu 100oC. Suhu sambungan
kedua logam adalah . . .
A. 90oC
B. 80oC
C. 75oC
D. 60oC
E. 50oC
Pembahasan
:
Diketahui
:
|
*Logam
dingin |
*Logam
panas |
||||
|
k1 |
= |
(1/4)k |
k2 |
= |
k |
|
Ti |
= |
0
oC |
Ti |
= |
100
oC |
|
Tf |
= |
X
oC |
Tf |
= |
X |
|
ΔT1 |
= |
Tf
– Ti |
ΔT2 |
= |
Tf
– Ti |
|
|
= |
(X-0) |
|
= |
(X-100)
atau |
|
|
|
|
|
|
(100-X) |
Ditanya : Suhu akhir atau
suhu setimbang pada sambungan (Tf )
|
Hpanas |
= |
Hdingin |
|
k2.A.ΔT2/L |
= |
k1.A.ΔT1/L |
|
k2.ΔT2 |
= |
k1.ΔT1 |
|
(k)(100-X) |
= |
(1/4)k(X-0) |
|
100-X |
= |
(1/4)X |
|
X |
= |
4(100-X) |
|
X |
= |
400
– 4X |
|
5X |
= |
400 |
|
X |
= |
80o |
Jawaban
B.
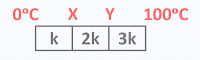
18. Tiga logam dengan ukuran yang sama disambung seperti gambar berikut!
Besar
suhu sambungan di Y adalah . . .
A. 900/17
B. 300/5
C. 900/13
D. 900/11
E. 90/1
Pembahasan
:
Diketahui :
|
kA |
= |
3k |
T3 |
= |
X
|
|
kB |
= |
2k |
T4 |
= |
0oC |
|
kC |
= |
k |
AA |
= |
AB
= AC = A |
|
T1 |
= |
100oC |
LA |
= |
LB
= LC = L |
|
T2 |
= |
Y |
|
|
|
Ditanya : Suhu di sambungan Y
(T2)
*Persamaan 1 antara logam
A dan B
|
HA |
= |
HB |
|
kA.AA.ΔTA/LA |
= |
kB.AB.ΔTB/LB |
|
kA.ΔTA |
= |
kB.ΔTB |
|
(3k)(T1-T2) |
= |
(2k)(T2-T3) |
|
3(100-Y) |
= |
2(Y-X) |
|
300-3Y |
= |
2Y
– 2X |
|
300 |
= |
5Y
– 2X |
*Persamaan 2 antara logam
B dan C
|
HC |
= |
HB |
|
kC.AC.ΔTC/LC |
= |
kB.AB.ΔTB/LB |
|
kC.ΔTC |
= |
kB.ΔTB |
|
(k)(T3-T4) |
= |
(2k)(T2-T3) |
|
(X-0) |
= |
2(Y-X) |
|
X |
= |
2Y
– 2X |
|
3X |
= |
2Y |
|
X |
= |
(2/3)Y |
*Subtitusi persamaan 1 dan
2
|
300 |
= |
5Y
– 2X |
|
300 |
= |
5Y
– 2((2/3)Y) |
|
300 |
= |
5Y
– (4/3)Y |
|
300 |
= |
(11/3)Y |
|
900/11 |
= |
Y |
|
Y |
= |
900/11 |
Jawaban
D.
19. Perhatikan
besaran besaran berikut ini!
1) Koefisien
radiasi
2) Emisivitas
bahan
3) Luas
permukaan
4) Konstanta
Boltzmann
Faktor
yang mempengaruhi besar rambatan kalor secara radiasi ditunjukkan oleh nomor .
. .
A. 1,
2, 3
B. 1,
3
C. 2,
4
D. 4
saja
E. semua
benar
Pembahasan
:
*Persamaan radiasi
I = e.A.σT4
T = suhu
σ = konstanta
Stevan-Boltzman
A = luas penampang
e = emisivitas bahan (koef)
Jadi, semua benar
Jawaban E.
20. Dua
ruangan berbentuk bola memiliki perbandingan jari-jari sebesar 100 : 1. Suhu
terkecil ruangan adalah 81 K. Jika kedua ruangan diharapkan memiliki besar
kalor radiasi yang sama, maka suhu ruangan lainnya perlu di-set sebesar . . .
A. 1,8
K
B. 3,0
K
C. 8,1
K
D. 16
K
E. 27
K
Pembahasan
:
Diketahui
:
T1
= 81 K
R1
: R2 = 1 : 100
Ditanya
: Suhu (T2)
|
I1 |
= |
I2 |
|
e.A1.σ.T14 |
= |
e.A2.σ.T24 |
|
e.(4πR12).σ.T14 |
= |
e.(4πR22).σ.T24 |
|
R12.T14 |
= |
R22.T24 |
|
1(814) |
= |
(1002)T24 |
|
T24 |
= |
4304,6721 |
|
T2 |
= |
8,1
K |
Jawaban
C.
Baca selanjutnya : 10 Soal & Pembahasan Teori Kinetik Gas (bagian 1) ǀ Pilihan Ganda
Itulah
10 soal dan pembahasan suhu, kalor, dan perpindahan kalor bagian 1. Klik
selanjutnya untuk soal dan pembahasan lainnya.