10 Soal & Pembahasan Fluida Dinamis (bagian 2) ǀ Pilihan Ganda
Sebelumnya, kita telah
membahas 10 soal fluida dinamis (bagian 1). Kita akan lanjutkan 10 soal fluida dinamis
(bagian 2). Berikut soal dan pembahasannya.
Baca
sebelumnya : 10 Soal & Pembahasan Fluida Dinamis (bagian 1) ǀ Pilihan Ganda
Pilihlah jawaban yang
tepat dari pilihan di bawah ini.
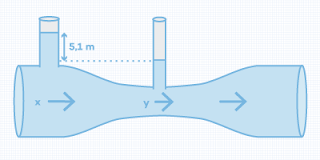
Perhatikan diagram
venturimeter di bawah ini!
11. Jika kelajuan air di X
adalah 2 m/s, maka kelajuan air di Y adalah . . .
A. 23,0 m/s
B. 32,0 m/s
C. 76,0 m/s
D. 10,3 m/s
E. 10,9 m/s
Pembahasan :
*Mencari perbedaan tekanan
pada pipa venturi
P1-P2 = (1/2) (ρ)(v22 - v12)
+ ρgΔy
P1-P2 = (1/2) (1000)(v22 – 22) + 0
P1-P2 = 500 (v22
– 4)
P1-P2 = 500 v22
– 2000
*Mencari tekanan tekanan dari tabung yang
memiliki selisih ketinggian h=5,1 m
P1-P2 = (1/2) (ρ)(v22 - v12)
+ ρgΔy
P1-P2 = (1/2) (ρ)(02 - 02) + ρgh
P1-P2 =0 + (1000)(10)(5,1)
P1-P2 =51000
*subtitusi persamaan 1 dan 2
51000
= 500v22 – 2000
500v22 = 53000
v2 = 10,3 m/s
atau kita dapat menggunakan persamaan cepat
v1 = akar (2gh/((A1/A2)2
- 1) dan
v2 = akar (2gh/((A1/A2)2
- 1)
Jawaban D.
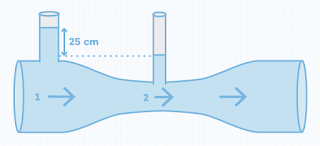
12. Gambar di bawah ini yang
menunjukkan air yang mengalir melewati pipa venturi.
Jika luas penampang A1
dan A2 masing-masing adalah 24 cm2 dan 16 cm2,
maka kecepatan air pada pipa besar adalah . . .
A. 5 m/s
B. 4 m/s
C. 3 m/s
D. 2 m/s
E. 1 m/s
Pembahasan
:
*Mencari
nilai v1
v1
= akar (2gh/((A1/A2)2 - 1)
v1
= akar (2.10.(0,25)/((24/16)2 - 1)
v1
= akar (5/(2,25- 1)
v1
= akar (5/(1,25)
v1
= akar (4)
v1
= 2 m/s
*kita
tidak perlu merubah satuan luas A1 dan A2 karena saling
bagi. Secara tidak langsung satuan akan hilang.
Jawaban
D.
13. Tangki
diisi air hingga kedalaman 15 m. Sebuah lubang kecil terdapat pada ketinggian
10 m dihitung dari dasar tangki. Besar kelajuan air yang memancar dari lubang
adalah . . .
A. 3,0
m/s
B. 10,0
m/s
C. 14,0
m/s
D. 17,1
m/s
E. 31,1
m/s
Pembahasan
:
*Persamaan
yang kita butuhkan hanya v = akar (2gh)
v
= akar (2gh)
v
= akar (2.10.5) = 10 m/s
*Penurunan
persamaan kelajuan air tangki atau pipa bocor pada hukum Torricelli didapat
dari
P1-P2 = (1/2) (ρ)(v22 - v12)
+ ρgΔy
P0-P0 = (1/2) (ρ)(v22 - 02) + ρgΔy
0 = (1/2) (ρ.v22 ) + ρg(y2- y1)
0
= (1/2) (ρ.v22 )
+ ρgy2- ρgy1
ρgy1 - ρgy2 = (1/2) (ρ.v22 )
ρg(y1- y2) = (1/2) (ρ.v22 )
ρg(h0 – h2) = (1/2) (ρ.v22 )
2ρgh1/ρ = v22
2gh1 = v22
v2
= akar (2gh1)
dimana,
h0 = panjang tangki mulai dasar – permukaan; h1 =
kedalaman kebocoran mulai lubang – permukaan; h2 = kedalaman kebocoran mulai
dasar – lubang
Jawaban B.
14. Gambar
dibawah ini menunjukkan peristiwa kebocoran pada tangki air.
Besar
kecepatan (v) air yang keluar dari lubang adalah . . .
A. akar
5 m/s
B. 2
akar 5 m/s
C. akar
10 m/s
D. 2
akar 10 m/s
E. 5
akar 2 m/s
Pembahasan
:
*Persamaan
yang kita butuhkan hanya x = 2 akar(h1.
h2) dan v = akar (2gh1)
x
= 2 akar(h1.
h2)
1
= 2 akar (h1.0,5)
12
= 22 (h1.0,5)
1
= 4 (h1.0,5)
h1
= 0,5 m
*Kelajuan
air
v
= akar (2gh1)
v
= akar (2.10.(0,5)) = akar 10 m/s
*Penurunan
persamaan x = 2 akar(h1. h2)
didapat dari
yf = yi
+ vi.t + ½ gt2
yf = 0 + 0.t +
½ gt2
yf = ½ gt2
h2 = ½ gt2
t = akar (2h2/g)
x = v.t
x2 = v2.t2
x2 = (2gh1). (2h2/g)
x2 = (4h1.h2)
x = 2 akar (h1.h2)
Jawaban
C.
15. Tangki yang terbuka diisi
dengan air sehingga tinggi air mencapai 6 m. Pada kedalaman 3 m dibawah
permukaan air, terdapat kebocoran kecil di sisi tangki sehingga air menyemprot
keluar dari lubang tersebut dan jatuh ke tanah sejauh R dari kaki tangki. Besar
jarak R adalah . . .
A. 2
m
B. 4
m
C. 6
m
D. 8
m
E. 10
m
Pembahasan
:
x = 2 akar (h1.h2)
x = 2 akar (3.3)
x
= 6 m
Jawaban
C.
16. Perhatikan
peristiwa kebocoran tangki air pada lubang P dari ketinggian tertentu pada
gambar dibawah ini. Jika besar percepatan gravitasi sebesar 10 m/s2,
maka air yang keluar dari lubang P akan jatuh ke tanah setelah . . .
A. akar
(5)/5 sekon
B. akar(5)/4
sekon
C. akar(5)/2
sekon
D. akar(5)
sekon
E. 2
akar(5) sekon
Pembahasan
:
*Kelajuan
air
v
= akar (2gh1)
v
= akar (2.10.(1)) = 2 akar(5) m/s
*Waktu
yang dibutuhkan untuk mencapai tanah. Kita dapat menggunakan persamaan t = x/v
atau t = vi sinθ/g, untuk gerak parabola di titik tertinggi.
t
= x/v
t
= 2/2 akar(5)
t
= 1/ akar(5) atau akar(5)/5, dengan mengalikan pembilang dan penyebut dengan
akar(5)
atau
t
= vi sinθ/g
t
= 2 akar(5) sin90/10
t
= akar(5)/5
Jawaban
A.
17. Tandon
air yang terbuka memiliki kedalaman 2 m. Sebuah lubang dengan luas penampang 10
cm2 dibuat di dasar tendon. Massa air per menit yang mula-mula akan
keluar dari lubang itu adalah. . .
A. (40)
akar 10 kg
B. (60)
akar 10 kg
C. (80)
akar 10 kg
D. (100)
akar 10 kg
E. (120)
akar 10 kg
Pembahasan
:
Pertama,
kita mencari kelajuan air yang keluar. Kedua, kita mencari debit air yang
keluar. Terakhir, kita mencari massa air yang keluar.
*Kelajuan
air
v
= akar (2gh1)
v
= akar (2.10.(2)) = 2 akar(10) m/s
*Debit
air
Q
= A.v
Q
= (10 x 10-4)( 2 akar(10))
Q
= 2 akar(10) x 10-3 m3/s
makna
debit di atas adalah terdapat 2 akar(10) x 10-3 volum air per detik
yang keluar, maka besar volumeya adalah 2 akar(10) x 10-3
*Massa
air yang keluar per detik
ρ = m/V
1000 = m/(2 akar(10) x 10-3)
m
= 2 akar(10) kg
jika
massa yang keluar per menit maka tinggal dikali 60 s = 120 akar(10) kg
Jawaban
E.
18. Pada
gambar berikut, air dalam tangki memancar keluar melalui lubang A dan membentuk
sudut 30o terhadap lantai. Jika pancaran air nya sampai di B, maka
tinggi air dalam tangki adalah . . .
A. (2/3)
akar 3 m
B. (4/3)
akar 3 m
C. (6/3)
akar 3 m
D. (8/3)
akar 3 m
E. (10/3)
akar 3 m
Pembahasan
:
Pertaman,
kita mencari kelajuan air keluar. Lalu, mencari kedalaman lubang pada tangki
dari permukaan dengan persamaan xmaks = vi2
sin 2θ/g; v = akar (2gh) atau v2 = 2gh
Pada
gerak parabola, xmaks = vi2 sin 2θ/g
xmaks
= vi2 sin 2θ/g
2
= vi2 sin 2(30)/10
2
= vi2 sin 60/10
2
= vi2 (akar(3)/2)/10
vi2
= 40/akar(3)
v2
= 2gh
40/akar(3)
= 2(10)h
h
= 2 akar(3)/3 atau
h
= (2/3) akar3
Jawaban
A
19. Pada
tabung pitot dialirkan gas dengan kelajuan v, sehingga perbedaan ketinggian
raksa pada kedua kaki manometer adalah 2 cm. Jika massa jenis gas sebesar 3, 4
kg/m3 dan massa jenis raksa 13600 kg/m3, maka besar nilai
v adalah . . .
A. 30
m/s
B. 40
m/s
C. 50
m/s
D. 60
m/s
E. 90
m/s
Pembahasan
:
v
= akar ((2.ρ’gh)/ρ)
v
= akar ((2.ρ’gh)/ρ)
v
= akar ((2.(13600)(10)(0,02))/3,4)
v
= akar (1600)
v
= 40 m/s
ρ’ adalah massa jenis pada
manometer dan ρ adalah massa jeis gas
Jawaban B.
20. Sebuah pesawat
terbang perlu dipercepat untuk mencapai kelajuan tertentu sebelum lepas
landas. Pada kondisi ini, perubahan momentum dari udara tegak lurus ke bawah
terhadap sayap dan sama besar dengan berat pesawat. Kelajuan udara mengecil seiring
dengan bertambahnya kelembapan udara. Pernyataan berikut ini yang benar adalah . . .
A. di hari yang lembab, kelajuan minimal lepas landas harus lebih besar karena kelembaban
udara lebih kecil
B. pada
hari yang lembab, kelajuan minimal lepas landas harus lebih kecil karena udara
mengembun dan mempunyai gaya hambat
C. kelajuan
minimum lepas landas harus konstan untuk hari lembab maupun kering
D. di hari yang kering, kelajuan minimum lepas landas harus lebih besar karena kelajuan
udara sekitar lebih besar
E. di hari yang kering, kelajuan minimum lepas landas harus lebih kecil karena tidak ada
pendingin sehingga massa pesawat menurun.
Pembahasan
:
Saat
pesawat terbang stabil, gaya angkat ke atas (Fa) = gaya berat
pesawat (Fb)
Fa
= Fg
Fa
= ΔP.A
Fa
= (1/2) (ρ)(v22 – v12).A
Fa
= (1/2) (ρ)( Δv).A
Saat
kelembapan udara meningkat atau menurun, massa jenis akan berubah. Akibatnya
gaya angkat ke atas akan berubah membesar atau mengecil. Sedangkan, gaya berat
Fg tidak berubah. Gaya angkat Fa akan tetap nilainya
walau kelembapan udara mengecil, jika kelajuan diperbesar, dimana udara lembab
= kelembapannya kecil.
Jadi,
saat hari lembab ρ=kecil
dan kelajuan harus diperbesar.
Jawaban A
Baca
selanjutnya : 10 Soal & Pembahasan Suhu, Kalor, & Perpindahannya (bagian 1) ǀ Pilihan Ganda
Itulah
10 soal dan pembahasan fluida dinamis seperti seperti debit fluida, pipa U, pipa
venturi, tabung pitot, dan kebocoran pipa. Klik selanjutnya untuk soal dan
pembahasan lainnya.